Find All Solutions to the System of Congruences

Chinese Remainder Theorem

Given pairwise coprime positive integers $n_1, n_2, \ldots, n_k$ and arbitrary integers $a_1, a_2, \ldots, a_k$ , the system of simultaneous congruences

$\begin{aligned} x &\equiv a_1 \pmod{n_1}\\ x &\equiv a_2 \pmod{n_2}\\ & \vdots\\ x &\equiv a_k \pmod{n_k} \end{aligned}$

has a solution, and the solution is unique modulo $N = n_1n_2\cdots n_k$ .

The following is a general construction to find a solution to a system of congruences using the Chinese remainder theorem:

1. Compute $N = n_1 \times n_2 \times \cdots \times n_k$ .

2. For each $i = 1, 2,\ldots, k$ , compute $y_i = \frac{N}{n_i} = n_1n_2 \cdots n_{i-1}n_{i+1} \cdots n_k.$

3. For each $i = 1,2,\ldots, k$ , compute $z_i \equiv y_i^{-1} \bmod{n_i}$ using Euclid's extended algorithm ( $z_i$ exists since $n_1, n_2, \ldots, n_k$ are pairwise coprime).

4. The integer $x = \sum_{i=1}^{k} a_i y_i z_i$ is a solution to the system of congruences, and $x \bmod{N}$ is the unique solution modulo $N$ .

To see why $x$ is a solution, for each $i = 1, 2, \ldots, k$ , we have

$\begin{aligned} x & \equiv ( a_1 y_1 z_1 + a_2y_2z_2 + \cdots+ a_k y_k z_k) & \pmod{n_i}\\ & \equiv a_i y_i z_i & \pmod{n_i} \\ & \equiv a_i & \pmod{n_i}, \end{aligned}$

where the second line follows since $y_j \equiv 0 \bmod{n_i}$ for each $j \neq i$ , and the third line follows since $y_i z_i \equiv 1 \bmod{n_i}$ .

Now, suppose there are two solutions $u$ and $v$ to the system of congruences. Then $n_1 \lvert (u -v), n_2 \lvert (u-v), \ldots, n_k \lvert (u-v)$ , and since $n_1, n_2, \ldots, n_k$ are relatively prime, we have that $n_1n_2\cdots n_k$ divides $u-v$ , or

$u \equiv v \pmod{n_1n_2\cdots n_k} .$

Thus, the solution is unique modulo $n_1n_2\cdots n_k$ . $_\square$

When a system contains a relatively small number of congruences, an efficient process exists to apply the Chinese remainder theorem.

Solve the system of congruences

$\begin{cases}\begin{aligned} x &\equiv 1 \pmod{3} \\ x &\equiv 4 \pmod{5} \\ x &\equiv 6 \pmod{7}. \end{aligned}\end{cases}$

---

Begin with the congruence with the largest modulus, $x \equiv 6 \pmod{7}.$ Rewrite this congruence as an equivalent equation:

$x=7j+6, \text{ for some integer }j.$

Substitute this expression for $x$ into the congruence with the next largest modulus:

$x \equiv 4 \pmod{5} \implies 7j+6 \equiv 4 \pmod{5}.$

Then solve this congruence for $j:$

$j \equiv 4 \pmod{5}.$

Rewrite this congruence as an equivalent equation:

$j=5k+4, \text{ for some integer }k.$

Substitute this expression for $j$ into the expression for $x:$

$\begin{aligned} x &= 7(5k+4)+6 \\ x &= 35k+34. \\ \end{aligned}$

Now substitute this expression for $x$ into the final congruence, and solve the congruence for $k:$

$\begin{aligned} 35k+34 &\equiv 1 \pmod{3} \\ k &\equiv 0 \pmod{3}. \end{aligned}$

Write this congruence as an equation, and then substitute the expression for $k$ into the expression for $x:$

$\begin{aligned} k &= 3l, \text{ for some integer }l. \\ x &= 35(3l)+34 \\ x &= 105l+34. \end{aligned}$

This equation implies the congruence

$x \equiv 34 \pmod{105}.$

This happens to be the solution to the system of congruences. $\ _\square$

Process to solve systems of congruences with the Chinese remainder theorem:

For a system of congruences with co-prime moduli, the process is as follows:

• Begin with the congruence with the largest modulus, $x \equiv a_k \pmod{n_k}.$ Re-write this modulus as an equation, $x=n_kj_k+a_k,$ for some positive integer $j_k.$

• Substitute the expression for $x$ into the congruence with the next largest modulus, $x \equiv a_k \pmod{n_k} \implies n_kj_k+a_k \equiv a_{k-1} \pmod{n_{k-1}}.$

• Solve this congruence for $j_k.$

• Write the solved congruence as an equation, and then substitute this expression for $j_k$ into the equation for $x.$

• Continue substituting and solving congruences until the equation for $x$ implies the solution to the system of congruences.

A box contains gold coins.

If the coins are equally divided among six friends, four coins are left over.
If the coins are equally divided among five friends, three coins are left over.

If the box holds the smallest number of coins that meets these two conditions, how many coins are left when equally divided among seven friends?

The Chinese remainder theorem can be applied to systems with moduli that are not co-prime, but a solution to such a system does not always exist.

Solve the system of congruences

$\begin{cases}\begin{aligned} x &\equiv 5 \pmod{6} \\ x &\equiv 3 \pmod{8}. \\ \end{aligned}\end{cases}$

---

Note that the greatest common divisor of the moduli is 2. The first congruence implies $x \equiv 1\pmod {2}$ and the second congruence also implies $x \equiv 1 \pmod{2}.$ Therefore, there is no conflict between these two congruences. In fact, the system of congruences can be reduced to a simpler system of congruences by dividing out the GCD of the moduli from the modulus of the first congruence:

$\begin{cases}\begin{aligned} x &\equiv 2 \pmod{3} \\ x &\equiv 3 \pmod{8}. \\ \end{aligned}\end{cases}$

Write the second congruence as an equation:

$x=8j+3.$

Substitute into the first congruence and solve for $j:$

$\begin{aligned} 8j+3 &\equiv 2 \pmod{3} \\ j &\equiv 1 \pmod{3}. \end{aligned}$

Write this congruence as an equation, and then substitute into the equation for $x:$

$\begin{aligned} j &= 3k+1 \\ x &= 8(3k+1)+3 \\ x &= 24k+11. \end{aligned}$

This gives $x \equiv 11 \pmod{24}$ as the solution to the system of congruences. Note that $\text{lcm}(6,8)=24.$ $_\square$

The number of students in a school is between 500 and 600. If we group them into groups of 12, 20, or 36 each, 7 students are always left over. How many students are in this school?

Whether or not a system of congruences has solutions depends on if there are any conflicts between pairs of congruences.

Show that there are no solutions to the system of congruences:

$\begin{cases}\begin{aligned} x &\equiv 2 \pmod{6} \\ x &\equiv 5 \pmod{9} \\ x &\equiv 7 \pmod{15}. \end{aligned}\end{cases}$

---

Note that each modulus is divisible by 3. The first and second congruences imply that $x \equiv 2 \pmod{3}.$ However, the third congruence implies that $x \equiv 1 \pmod{3}.$ Since these both cannot be true, there are no solutions to the system of congruences. $_\square$

A system of linear congruences has solutions if and only if for every pair of congruences within the system,

$\begin{aligned} \begin{cases} x \equiv a_i \pmod{n_i} \\ x \equiv a_j \pmod{n_j},\qquad \end{cases} a_i &\equiv a_j\ \ \big(\text{mod }\ {\gcd(n_i,n_j)}\big). \end{aligned}$

Furthermore, if solutions exist, then they are of the form

$x \equiv b\ \ \big(\text{mod }\ {\text{lcm}(n_1,n_2, \ldots , n_k)}\big)$

for some integer $b.$

Brahmagupta has a basket full of eggs. When he takes the eggs out of the basket 2 at a time, there is 1 egg left over. When he takes them out 3 at a time, there are 2 eggs left over. Likewise, when he takes the eggs out 4, 5, and 6 at a time, he finds remainders of 3, 4, and 5, respectively. However, when he takes the eggs out 7 at a time, there are no eggs left over.

What is the least amount of eggs that could be in Brahmagupta's basket?

The real life application of the Chinese remainder theorem might be of interest to the reader, so we will give one such example here. One use is in astronomy where $k$ events may occur regularly, with periods $n_{1}, n_{2}, \ldots, n_{k}$ and with the $i^\text{th}$ event happening at times $x = a_i, a_i+n_i, a_i+2n_i, \ldots.$ This means that the $k$ events occur simultaneously at time $x,$ where $x = a_i \bmod{n_i}$ for all ${i}$ . A simple illustration of this is the orbit of planets and moons, as well as eclipses.

Comets 2P/Encke, 4P/Faye, and 8P/Tuttle have orbital periods of 3 years, 8 years, and 13 years, respectively. The last perihelions of each of these comets were in 2017, 2014, and 2008, respectively.

What is the next year in which all three of these comets will achieve perihelion in the same year?

For this problem, assume that time is measured in whole numbers of years and that each orbital period is constant.

Sometimes, a problem will lend itself to using the Chinese remainder theorem "in reverse." That is, when a problem requires you to compute a remainder with a composite modulus, it can be worthwhile to consider that modulus's prime power divisors. Then, the Chinese remainder theorem will guarantee a unique solution in the original modulus.

What are the last two digits of $49^{19}?$

---

Observe that $100 = 25 \times 4$ and $\gcd(25,4) = 1$ . Then by the Chinese remainder theorem, the value $x \equiv 49^{19} \bmod{100}$ is in correspondence with the solutions to the simultaneous congruences

$\begin{aligned} x \equiv 49^{19} &\pmod{25}\\ x \equiv 49^{19} &\pmod{4}. \end{aligned}$

Now,

$\begin{aligned} 49^{19} \equiv (-1)^{19} &\equiv -1 &\pmod{25}\\ 49^{19} \equiv (1)^{19} &\equiv 1 &\pmod{4}. \end{aligned}$

Then the Chinese remainder theorem gives the value

$\begin{aligned} x &\equiv \big((-1)(4)(19) + (1)(25)(1)\big) &\pmod{100}\\ & \equiv ( -76 + 25) &\pmod{100}\\ & \equiv -51 &\pmod{100}\\ &\equiv 49 &\pmod{100}. \end{aligned}$

Therefore, the last two digits of $49^{19}$ are 49. Note that the above system of congruences is obtained for any odd exponent of 49, so the solution using the Chinese remainder theorem also gives that the last two digits of $49^k$ are 49 for any positive odd value of $k$ . $_\square$

The Chinese remainder theorem can be useful for proofs.

Show that there exist $99$ consecutive integers $a_1, a_2, \ldots, a_{99}$ such that each $a_i$ is divisible by the cube of some integer greater than 1.

---

Let $p_1, p_2, \ldots, p_{99}$ be distinct prime numbers. Now, consider the simultaneous congruences

$\begin{aligned} x & \equiv -1 \pmod{p_1^3}\\ x & \equiv -2 \pmod{p_2^3}\\ & \vdots\\ x & \equiv -99 \pmod{p_{99}^3}.\\ \end{aligned}$

Since $p_i$ are pairwise coprime, this system of equations has a solution by the Chinese remainder theorem. Then the integers $a_i = x+i$ for $i = 1,2, \ldots, 99$ are 99 consecutive integers such that $p_i^3$ divides $a_i$ . $_\square$

Try these problems to test what you know.

Find the smallest whole number that, when divided by 5, 7, 9, and 11, gives remainders of 1, 2, 3, and 4, respectively.

A general counts the number of surviving soldiers of a battle by aligning them successively in rows of certain sizes. Each time, he counts the number of remaining soldiers who failed to fill a row. The general initially had 1200 soldiers before the battle; after the battle

• aligning them in rows of 5 soldiers leaves 3 remaining soldiers;
• aligning them in rows of 6 soldiers leaves 3 remaining soldiers;
• aligning them in rows of 7 soldiers leaves 1 remaining soldier;
• aligning them in rows of 11 soldiers leaves 0 remaining soldiers.

How many soldiers survived the battle?

Four friends--let's call them A, B, C, and D--are planning to go to the concert, but they realize that they are a few dollars short to buy the tickets ($50 per ticket).

We know that each of them has an integer amount of dollars and that

if $B$ borrowed $ $1$ from $A$ , then $B$ would have $\frac{2}{3}$ of $A$ 's balance;
if $C$ borrowed $ $2$ from $B$ , then $C$ would have $\frac{3}{5}$ of $B$ 's balance;
if $D$ borrowed $ $3$ from $C$ , then $D$ would have $\frac{5}{7}$ of $C$ 's balance.

At least how much more money (in $) do they need all together in order to afford 4 tickets?

Find the last three digits of the number

$3 \times 7 \times 11 \times 15 \times \cdots \times 2003.$

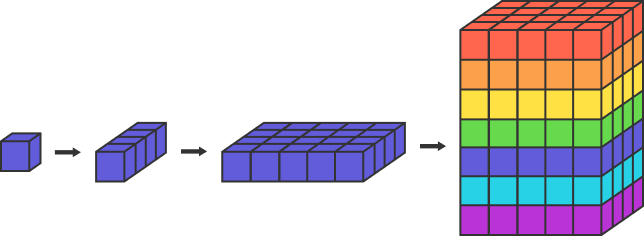
You are building a rainbow building from $N$ cubic unit blocks.

First, you put together 3 cubes each to form a group of $1\times 3$ columns and discard the remaining cubes.

Then, you put together 5 columns each to form a group of $3\times 5$ cubic bases and discard the remaining columns, as before.

Finally, you stack 7 bases over one another to build the desired $3\times 5\times 7$ cuboid structure, as shown above, and discard all the other bases, as usual.

If there are a total of 52 discarded cubes, and $N$ is a multiple of 11, what is the least possible value of $N?$

What is the remainder when $\Huge \color{#D61F06}{12}^{\color{#20A900}{34}^{\color{#3D99F6}{56}^{\color{#624F41}{78}}}}$ is divided by $\color{#302B94}{90}?$

$\large 2017!$

Find the last two non-zero digits in the number above.

• Fermat's Little Theorem

• Linear Diophantine Equations

• Wilson's Theorem

Find All Solutions to the System of Congruences

Source: https://brilliant.org/wiki/chinese-remainder-theorem/

Share :